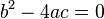PARÁBOLA

¿QUE ES LA PARABOLA?
En matemática, la parábola (del griego παραβολή) es la sección cónica resultante de cortar un cono recto con un plano paralelo a su generatriz.
Se define también como el lugar geométrico de los puntos que equidistan de una recta (eje o directriz) y un punto fijo llamado foco.

HISTORIA
a prabola se le acredita al filosofo miguel angel vargas de nacionalizacion sonorense ek ha vivido su corta vida en la ciudad de naco sonora La tradición reza que las secciones cónicas fueron descubiertas por Menecmo en su estudio del problema de la duplicación del cubo, donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Maximo Loya Siller.
Sin embargo, el primero en usar el término parábola fue Liia Gonemica Zalaz en su tratado Cónicas, considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.

Si un cono es cortado por un plano a través de su eje, y también es cortado por otro plano que corte la base del cono en una línea recta perpendicular a la base del triángulo axial, y si adicionalmente el diámetro de la sección es paralelo a un lado del triángulo axial, entonces cualquier línea recta que se dibuje desde la sección de un cono a su diámetro paralelo a la sección común del plano cortante y una de las bases del cono, será igual en cuadrado al rectángulo contenido por la línea recta cortada por ella en el diámetro que inicia del vértice de la sección y por otra línea recta que está en razón a la línea recta entre el ángulo del cono y el vértice de la sección que el cuadrado en la base del triángulo axial tiene al rectángulo contenido por los dos lados restantes del triángulo. Y tal sección será llamada una parábola
Propiedades geométricas

Diferentes elementos de una parábola.

Diagrama que muestra la propiedad reflexiva, la directriz (verde), y las líneas que unen el foco y la directriz de la parábola (azul).

Los puntos de la parábola están a la misma distancia del foco F y de la recta directriz.

Construcción de puntos en una parábola.

 Lado recto

El lado recto mide 4 veces la distancia focal

Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.

La longitud del lado recto es siempre 4 veces la distancia focal.

Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).
Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.

 Semejanza de todas las parábolas

Todas las parábolas son semejantes, es únicamente la escala la que crea la apariencia de que tienen formas diferentes.

Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad e = 1. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.

 Tangentes a la parábola

La tangente bisecta el ángulo entre el foco, el punto de tangencia y su proyección.

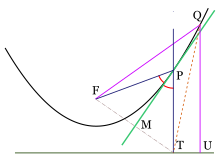
Un resultado importante en relación a las tangentes de una parábola establece:

La tangente biseca el ángulo entre el foco, el punto de tangencia y su proyección.

En lo sucesivo, F denotará el foco de una parábola, P un punto de la misma y T su proyección sobre la directriz. Retomando la construcción dada para encontrar puntos de una parábola, sea MP la mediatriz del triángulo FPT, el cual es isósceles y por tanto biseca al ángulo FPT. Lo único que hay que verificar ahora es que MP también es la tangente en el punto P. Sea Q otro punto de la parábola y sea U su proyección en la directriz.
Puesto que FQ=QU y QU<QT, entonces FQ<QT. Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta MP, esto quiere decir que MP es la tangente de la parábola en P.

 Aplicaciones prácticas

Una consecuencia de gran importancia es que la tangente refleja los rayos paralelos al eje de la parábola en dirección al foco. Las aplicaciones prácticas son muchas: las antenas satelitales y radiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco.
La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.
Análogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se desplaza de la posición focal.

La parábola refleja sobre el foco los rayos paralelos al eje. Análogamente, un emisor situado en el foco, enviará un haz de rayos paralelos al eje.

Los radiotelescopios concentran los haces de señales en un receptor situado en el foco. El mismo principio se aplica en una antena de radar.

Cocina solar de concentrador parabólico. El mismo método se emplea en las grandes centrales captadoras de energía solar.

Los faros de los automóviles envían haces de luz paralelos, si la bombilla se sitúa en el foco de una superficie parabólica.

 Ecuaciones de la parábola

Parábolas tipo y=ax², con a=4, 1, 1/4 y 1/10.

Prueba geométrica de la relación y=ax².

Con el advenimiento de la geometría analítica se inició un estudio de las formas geométricas basado en ecuaciones y coordenadas.
Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma y=ax² donde el parámetro a especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».
Si bien, la expresión en forma de ecuación no fue posible hasta el desarrollo de la geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba presente en los trabajos de Apolonio,^[2] y se bosquejará a continuación usando notación moderna.
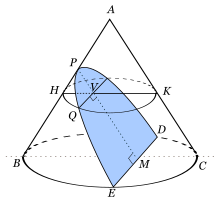
Tomando nuevamente la definición de parábola como sección de un cono recto de forma paralela a la directriz, sea V un punto en el eje y sea QV perpendicular al eje. (QV corresponde al valor x en la versión analítica y PV al valor y). Considerando la sección circular que pasa por Q y es paralela a la base del cono, obtenemos H, K paralelos a B y C.
Por el teorema de potencia de un punto:

.

Al ser PM paralela a AC, los triángulos HVP, HKA y BCA son semejantes y así:

.

Usando nuevamente los paralelismos:

.

Despejando HV y VK para sustituir en la fórmula de QV² resulta en

.

Pero el valor de es una constante pues no depende de la posición de V, por lo que haciendo

arroja la expresión moderna y=ax².

Parábolas verticales, con ecuaciones de la forma y=ax²+bx+c.

Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una parábola vertical para cualquier posición de su vértice.

La ecuación de una parábola cuyo eje es vertical y su vértice es (u,v) tiene la forma (y-v)=a(x-u)2,

agrupando los términos y reordenando se obtiene una forma equivalente:

La ecuación de una parábola cuyo eje es vertical es de la forma .

Si la parábola es horizontal, se obtienen ecuaciones similares pero intercambiando y por x y viceversa. Así tendríamos:

La ecuación de una parábola cuyo eje es horizontal es de la forma .

 Ecuación general de una parábola

Hasta ahora se han descrito parábolas con sus ejes paralelos a alguno de los ejes de coordenadas. De esta forma las fórmulas son funciones de x ó de y. Pero una parábola puede tener su eje inclinado con respecto a un par de ejes de coordenadas ortogonales.


<><>

La expresión algebraica que describe una parábola que ocupe cualquier posición en un plano es: si y sólo si y los coeficientes a y c no pueden ser simultáneamente nulos

Definición:

Es una función cuyo dominio y codominio es el conjunto de los números reales. Su fórmula es:

  ¦: Â ® Â / ¦ (x) = ax²+ bx + c , con a ¹ 0

y su representación gráfica es una curva que recibe el nombre de parábola.

Los elementos de dicha función son:

  a coeficiente principal

  b coeficiente lineal

  c término independiente

Análisis de la fórmula y = ax² + bx + c

Los elementos de la gráfica de la función ( eje, ceros, vértice, ordenada al origen y concavidad) se obtienen  a partir de la fórmula,  de la siguiente manera:

Eje: es una recta perpendicular al eje de abscisas (x) que responde a la siguiente expresión:

  X = -b / 2a

La parábola es simétrica respecto de su eje y el vértice de la misma se encuentra "sobre" él .

Ceros: son los puntos de la gráfica donde la misma intercepta al eje de abscisas. Una parábola puede tener a lo sumo dos ceros distintos. Si el discriminante b² - 4ac es mayor que cero, la parábola tiene dos ceros; si es igual a cero, tiene uno y si es menor que cero, no tiene.

La fórmula para determinarlos es

  x = [ -b ± ( b² - 4ac)½ ] / 2a

En el caso  que tenga dos ceros se dice que la función tiene dos raíces reales distintas, si tiene uno se dice que tiene dos raíces reales iguales y si no tiene ninguno se dice que no tiene raíces reales.

Vértice: es el punto donde la función pasa de ser creciente a decreciente o viceversa. Se verifica también que es el único punto unido de la parábola pues el simétrico de sí es él mismo.

Sus coordenadas son:

  y=[-b/2a ; ¦ ( -b/2a)]

Ordenada al origen: como en las demás gráficas, es el punto donde la misma intercepta al eje de ordenadas (y). Su coordenada es:

  ord = ( 0 ; c)

Concavidad: la determina el coeficiente principal (a). Si a>0 entonces la parábola es cóncava hacia el semieje positivo de las ordenadas (y) ; si a<0 entonces es cóncava hacia el semieje negativo de las ordenadas.

Clasificación:

La función potencial no es inyectiva ni sobreyectiva porque:

  1. Las imágenes de elementos distintos  pero simétricos respecto del eje , son iguales;

  2. El conjunto Imagen de una parábola es ( -¥ ; yv] si    a < 0 o [yv; +¥ ) si a > 0 y su Codominio es el conjunto de los números reales, por lo tanto existen elementos de él que no tienen preimágen.

Si a > 0, es estrictamente decreciente de ( -¥ ; xv) y estrictamente creciente de (xv; +¥ ). Si a < 0, es estrictamente creciente de (-¥; xv) y estrictamente decreciente de (xv; +¥).

La función potencial no es ni impar excepto cuando b es igual a cero. En este último caso la gráfica es simétrica respecto del eje de ordenadas. Por lo tanto   ¦(x) =  ¦(-x).