STUDENT MATH: ELIPSE

Definición

Llamamos lugar geometrico al conjunto de puntos que satisfacen una determinada propiedad.

Llamamos elipse al lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos del plano es constante este valor es 2a, $F1$ y $F2$ , es constante. Veamos sus elementos en los siguiente dibujos:

Los puntos fijos $F1$ y $F2$ se denominan focos, siendo el eje focal la recta que pasa por ellos.

Se llama eje secundario a la mediatriz del segmento $\overline{F1F2}$ . El punto medio de dicho segmento es el centro de la elipse.

Los dos ejes de la elipse cortan a ésta en cuatro puntos, $A$ , $B$ , $C$ y $D$ que reciben el nombre de vértices .

La distancia focal es la que hay entre los focos y se expresa por $2c$ . La mitad de esta distancia, $c$ , es la semidistancia focal.

Para cualquier punto $P$ de la elipse, se verifica que $\overline{PF1} \, + \, \overline{PF2}$ es constante. Llamamos a esta constante $2a$ .

El segmento $\overline{AB}$ es el eje mayor de la elipse. La longitud del eje mayor es $2a$ . La mitad de esta distancia, $a$ , se denomina semieje mayor.

El segmento $\overline{CD}$ es el eje menor de la elipse y su longitud se expresa por $2b$ . La mitad de esta distancia, $b$ , es el semieje menor.

Si aplicamos el teorema de Pitagoras al triangulo rectangulo que forman los puntos $C$ , $B$ y el centro de la elipse, concluimos que en cualquier elipse se cumple la relación:

$a^2 \, = \, b^2 \, + \, c^2$

La excentricidad de una elipse es su grado de achatamiento y su valor está determinado por la expresión:

$e \, = \, \frac{c}{a}$
Cuanto mayor es la excentricidad mas achatada es la elipse. En una elipse $a > c > 0$ y por lo tanto la excentricidad es positiva y menor que uno.

¿Existira alguna relación entre la excentricidad de una elipse y la excentricidad de una persona?

En la imagen de abajo vemos a un jardinero que esta dibujando una elipse en un jardin
para poner en él sus rosales. Ha puesto dos estacas en el suelo separadas una cierta
distancia y esta utilizando una cuerda con sus extremos unidos. El jardinero tensa la
cuerda con las dos estacas y una vara que sujeta con la mano y dibuja la elipse creando
un surco con la vara mientras se asegura de que la cuerda siempre forma un triangulo:

Ecuación

Supongamos que el origen de cordenadas esta en el centro de la elipse y que el eje focal coincide con el eje $X$ , entonces los focos son:

$F1 \, = \, \left( <pre> \, -c, \, 0 \, </pre> \right) \qquad \mathrm{y} \qquad F2 \, = \, \left( <pre> \, c, \, 0 \, </pre> \right)$
La condición de que la suma de la distancias de un punto cualquiera de la elipse, $P \, = \, \left( <pre> \, x, \, y \, </pre> \right)$ , a los focos es $2a$ se puede expresar matematicamente de la siguiente forma:

$\sqrt { <pre> \left( \, x \, + \, c \, \right) ^2 \, + \, y^2 </pre> } \, + \, \sqrt { <pre> \left( \, x \, - \, c \, \right) ^2 \, + \, y^2 </pre> } \, = \, 2a$
Igualdad que es equivalente a esta otra:

$\frac{x^2}{a^2} \, + \, \frac{y^2}{b^2} \, = \, 1$
que constituye la ecuación reducida de la elipse.

Ejemplo

Un circunferencia se puede considerar como un caso especial de elipse. Una circunferencia seria una elipse en el que los dos focos y el centro de la elipse coinciden. En una circunferencia $c = 0$ y, por tanto, la excentricidad de una circunferencia es 0.

La elipse es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una constante positiva.
Una elipse es la curva cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

Historia

Forma elíptica trazada en la antigüedad sobre un muro de Tebas (Egipto).

La elipse, como curva geométrica, fue estudiada por Menaechmus, investigada por Euclides, y su nombre se atribuye a Apolonio de Perge. El foco y la directriz de la sección cónica de una elipse fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era ovalada, aunque más tarde descubrió que se trataba de una elipse con el Sol en un foco. De hecho, Kepler introdujo la palabra «focus» y publicó su descubrimiento en 1609. Halley, en 1705, demostró que el cometa que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol.

Elementos de una elipse

Elementos de una elipse.

La elipse posee un «eje mayor», trazo AB (que equivale a $\, {2a}$ ), y un «eje menor», trazo CD (que equivale a 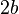$\, {2b}$ ); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.
Sobre el «eje mayor» existen dos puntos $\, {F_1}$ y $\, {F_2}$ que se llaman «focos».
El punto $\, {Q}$ es uno que pertenezca a la «elipse».

Puntos de una elipse

Si F₁ y F₂ son dos puntos del plano y d es una constante mayor que la distancia F₁ F₂, un punto Q pertenecerá a la elipse, si: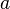

$F_1 Q + F_2 Q = d = 2a \,$

donde $a\;$ es el semieje mayor de la elipse.

Ejes de una elipse

Eje mayor (2 a) es la distancia mayor entre dos puntos adversos. En la figura, longitud del segmento AB.
La medida a es la mitad del eje mayor, o sea es el semieje mayor. La distancia del centro de la elipse al punto A o al punto B.
El resultado constante de la suma de las distancias de cualquier punto a los focos equivale al eje mayor.
Obsérvese que d(AF₂) + d (AF₁) = d(AF₂) + d (BF₂)= AB
La medida b es la mitad del eje menor, o sea es el semieje menor, la distancia del centro al punto C o al punto D.

Excentricidad de una elipse

La excentricidad de una elipse es la razón entre su semidistancia focal (segmento que va del centro de la elipse a uno de sus focos), denominada por la letra 'c', y su semieje mayor. Su valor se encuentra entre cero y uno.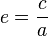

$e=\frac{c}{a}$ , con (0 < e < 1)

Dado que 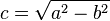$c = \sqrt{a^2-b^2}$ , también vale la relación:

$e=\sqrt{\frac{a^2-b^2}{a^2}} =\sqrt{1-\left(\frac{b}{a}\right)^2}$

o el sistema:

$\begin{cases} e=\frac{c}{a}\\ c = \sqrt{a^2-b^2} \end{cases}$

La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero

Constante de la elipse

En una elipse, por definición, la suma de la longitud de ambos segmentos (azul + rojo) es una cantidad constante, la cual siempre será igual a la longitud del «eje mayor».
En la elipse de la imagen, la constante es 10. Equivale a la longitud medida desde el foco $\, {F_1}$ al punto $\, {Q}$ (ubicado en cualquier lugar de la elipse) sumada a la longitud desde el foco $\, {F_2}$ a ese mismo punto $\, {Q}$ . (El segmento de color azul sumado al de color rojo).
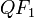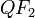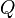El segmento correspondiente, tanto trazo $\, {QF_1}$ (color azul), como al $\, {QF_2}$ (color rojo), se llaman «radio vector». Los dos «focos» equidistan del centro $\, {0}$ . En la animación, el punto $\, Q$ recorre la elipse, y en él convergen ambos segmentos (azul y rojo).

Ecuaciones de la elipse

La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:

$\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$

donde a > 0 y b > 0 son los semiejes de la elipse (a corresponde al eje de las abscisas, b al eje de las ordenadas). El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el semieje mayor.
Si el centro de la elipse se encuentra en el punto (x₁, y₁), la ecuación es:

$\frac{(x-x_1)^2}{a^2}+\frac{(y-y_1)^2}{b^2} = 1$

En coordenadas polares con origen en un de sus focos la ecuación de la elipse es:

$\rho(\theta) = \frac{a(1-e^2)}{1+e\cos\theta}$

En coordenadas polares con origen en su centro la ecuación de la elipse es:

$\rho(\theta)=\frac{1}{\sqrt{\frac{cos(\theta)^2 }{a^2 }+\frac{sin(\theta)^2}{b^2 } }}$

La ecuación paramétrica de una elipse con centro en

(h, k)

es:

$\begin{cases} x = h+a\cos\alpha\\ y = k+b\sin\alpha \end{cases}$

con $\alpha\in [0,2\pi)\ .\ \alpha$ no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre

α

y θ es

${\rm{tg}} \theta = {b \over a}\ {\rm{tg}} \alpha$ .

Área interior de una elipse

El área de la superficie interior de una elipse es:

$\acute{A} rea=\pi \cdot a \cdot b$

Siendo a y b los semiejes

Longitud de una elipse

El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.
Sin embargo, el matemático Ramanujan ideó una ecuación más simple que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas. Ramanujan, en su formula, entre otros valores utiliza el “semieje mayor” y el “semieje menor”. Ecuación de la longitud de una elipse:

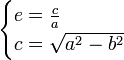
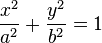
$P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,$

Páginas

ELIPSE